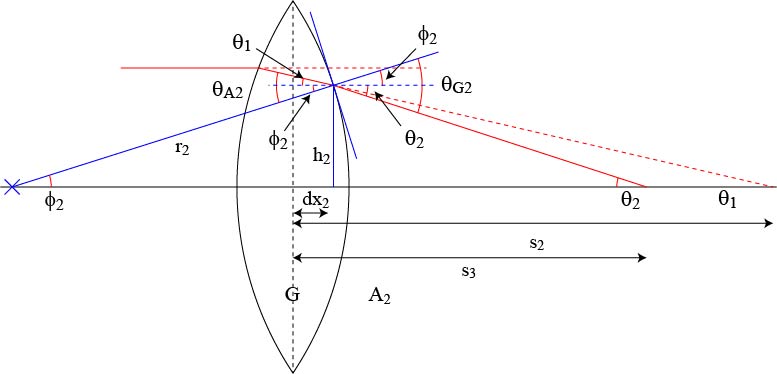
今度は以下の図のようなレンズ内(G)から外(A2)に出て行く光線を考えましょう.

さらに...結構複雑ですね....
まずは,それぞれの記号の説明をしましょう.
φ2 : 光線がレンズ左側に当たった場所の曲率半径の軸に対する角度
r2 : 曲率回転半径
h2 : そのときの高さ
dx1 : そのときのレンズ中心からのずれ
θ1 : 光線が屈折しないとして軸と交わる点での角度
θ2 : 屈折した光線が軸と交わる点での角度
s3 : 屈折した光線が軸と交わる点の距離
θA2 : 入射角
θG2 : 屈折角
です.
幾何学的な関係は,近似を考えると,
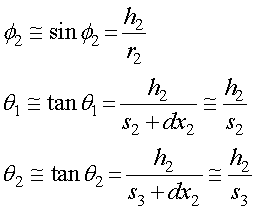
となります.
ここで,θ1,は前ページではh1/s2,で計算していましたが,今回はh2を使います.
また,屈折の関係から,

.また,

これらを代入することにより,

と,s3,を求めることができました.ここで曲率の定義からr2にマイナスが入っていることに注意しましょう.
ここで,s2は前ページで求めましたので,
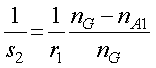

今回求めたs3とは平行光を入射した場合の軸との交点の位置なので,焦点,そのものですね.ですので,
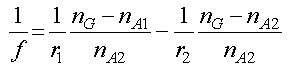
となります.
もし,A1,A2が空気なら,nA1=nA2=1,となるので,

これがレンズメーカーの式となります!
次に,レンズの曲率と焦点距離との関係を求めてみましょう.